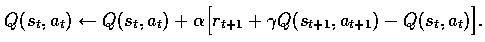
The probabilistic nature of the game makes it an interesting problem for learning algorithms, though the problem of learning a good playing strategy is not obvious.I think that yatzhee serves a good example for learning strategies with reinforcement learning techniques.
This program implements a simplified version of the game of Yatzee The game is for One player.Further more, not all thirteen combinations are needed but only four: Three Of a kind, Four a kind, Big Yathzee & Small Yathzee.
The algrothim used is SARSA algorithm.
The algorithm is an on-line algorithm. It has a set of states (S).
Each state has a set of action (A) that it can do.
The last input is a value function (r(s,a)).
The algorithm samples in each new turn (t+1) a new state and action and updates
global set of values (Q) of the previous turn (t) due to the formula:
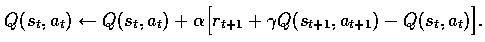
The set of states is all dice combinations which appear in any subgroup of five dices. The order of the combination doesn't matter and it includes repetitions(e.g "666" counts). The statistical compution involves Niyutons' Binomial results 467 states. When discarding of all the five dices states, the number of states decreases to 209. We can eliminate those state and treat them as one "end" state
As for the set of actions. In first appearence there seem to be two actions: choose dice and finish round, but those action don't give us any information. When examine the problem we see those action are actually the same. To "finish round" is actually to choose all dices.So now there is only one action, but in order to gain information there must be more then one action. I took a naive approach and consider every dice combination without order considiration to be an action. That result, as in the number of states calculation, 467 actions. In order to decrease the number of actions I shrinked all five-dice actions that are not a valid yatzee combination to the same state. As result the number of actions droped to 228.
For the value function. It seems resonable to give the value of yatzee game to the states. That means that if a the dice combinations when unifying the state and action dices are a valid Yatzee combination the immidiate value is the score of the turn in the game. Other wise if it is not a yathzee combination the value is zero. That was the values i first used but it is a bit problematic as I explain in the observation section.
Below you can see how the algorithm works.
The grey text box are the dice thrown each round.
Each state has a dice combination.
Action is the subgroup taken from the thrown dices(scribed the arrows).
The turn is finished when all 5 dices are chosen.
It ends with the start state if the 5 dice combination is not valid yathzee combination.
Otherwise it ends in the "end" state if it is a yathezee combination.

The last component is the yathzee categories. After scoring Yathzee combination you can't score it again in the game. Beacuse of that notion the combination of the categories also counts. In order for the game to be complete the scored categories must be taken as part of the states. The categories combination number is 2^13. That factor makes the model too large. That is why i took only four categories. 2^4 makes the number of states to be multiplied by 16, so we have about 2000 states. The only change now is that the game is finished only after all four categories are chosen.
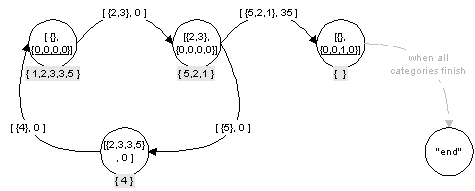
Below you can see how the algorithm works with categories.
Each state has category beside dice combination.
If scored a yathzee category it moves to the next yathzee combination.
If the 5 dice combination is not yathzee combination it starts another turn in with the same category.
You can see that the 5-dices state are not needed in the program.
The method of testing is very simple. I let the computer play against itself for trials of one hundrend games each. for each trial I took a simple statistics of the average number of turns it took the computer to finish the games. I also took the average points the computer scored in the games. Then I checked if the avarages of the trials have improved from one trial to another and how fast. The statistics was dumped automatically into a summery file. After the computer learned the game I also tested it manually and checked if it palyed with a "common sense", e.g. if it acted as "real" player.
In order to save run time I devided the testing into two categories. In the first phase used a simplified version that contained only one yathzee category the three-in-a-raw. It is a "good" category to do the testing on beacuse statistically it is quite a common category, so the computer can learn it quickly. Another reason to choose three-in-a-row is that the number of points is not fixed, e.g 4-4-4-3-2 scores 12 but 5-5-5-6-2 scores 15. In the first phase the computer made 100 trials in a run.
At the second phase I tested all four categories. Each run also had 100 trials but I increased the number of games per trial to 1000. Those runs took much more time beacuse the number of turns requested too finish a game has increased. It also took more trials for the computer to learn beacuse the number of entries in the global set of values(Q) was sixteens times bigger
The game of yathzee has two criterias of winning. You can win by finishig scoring all yathzee combination first. It means you do it in less turns as possible. On the other hand for each combination you score points. If you finish the game together with your opponent or play alone what matters is the number of points you scored. In the first testing pahse I used the three-in-a-raw category to reach balance between the two criterias of winning. The first "naive value function" I used "gained" the yathzee combinations their "real" value but didn't "punished" other combinations (zero value). It just retruned zero for evry state other then yatzee combinatios states. It caused computes policy to make very high avarage number of points in the trials. For example, when I used random policy the avarage score was about 10. At the end of the learning trials the naive value functions policy avarage score was 16. The problem was the number of turns. In both cases the number of turns till the combination scored was 4. I did a series of experiments to choose the correct punishment. I used -5,-10, negative values for the five-dice combinations that are not three-in-a-raw. The number of turns decreased but it made also the points number decrease. With -5 punishment the turn avarge is two and score avarge is thirteen. With -10 punishment the turn avarges is less then two and the score avrage remianes the same. summery log of three-in-a-row learning with -10 punishment
The parameters were chosen also in the first phase of testing.
In this phase I tested the computer learning of yatzee game with four categories. I compaired the SARSA policy learning with the paramters above against a random policy. The random policy finished the game in avarage of 68 turns and avarge points number of 82. The learning policy finished in avarge of 19 turns per game!. The score number improved a little to 84. summery log of four categories learning
the program is written as java thread. It demonstares how the computer play yatzee aftre the lerning trials. every two seconds the program play another round and prints it to the screen. The learning trials Q-value table is in 'state-action.save' file. If you want to see how the program acts without learning you can remove the file. Other resource files are the 'states', 'actions' and 'categories' files, they store the indexes of the states and the action. 'Summery' is a log created during the run with the statistics on the runs turns number & scores.
The following zip file contain the program yathzee.zip