
Combination system: The outputs at any instant of time are functions only of the input at that time.
Sequential system: The output at time t is a function of the input at time t , the output at time t-1 and the internal state.
Memory device:
- Zi – output: Zi = fi(x(0),x(1),.....x(n-1),y(0),.....,y(n-1))
- Xi – input.
- present state: {y(0), y(1), ...... , y(k-1)}
- next state: {Y(0), Y(1), ...... , Y(k-1)} such that Y(i) = gi(x(0),x(1),.....x(n-1),y(0),.....,y(n-1))
- Boolean functions
- State diagram
- State table
- Timing diagram
There are two basic ways to organize a clocked sequential network:
- Moore machine: The outputs depend only on the present state.
The outputs are computed by a combinational
logic block whose only inputs are the flip-flops' state outputs. The outputs
change synchronously with the state transition and the clock edge.

- Mealy machine: The outputs depend on the present state and
the present value of the inputs.

The outputs can change immediately after a change at the inputs, independent of the clock. A Mealy machine constructed in this fashion has asynchronous -outputs.
Example: Sequential system that detects a sequence of 1111:
STEP 1:state diagram
– Mealy circuit
The next state depends
on the input and the present state.
Non overlapping detection:
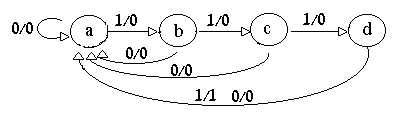
Overlapping detection:
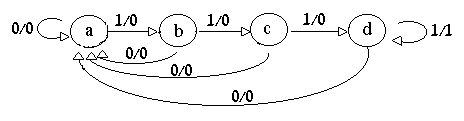
STEP 2:State table.
Converting the state
diagram into a state table: (Overlapping detection)
It contains present
state (p.s) and next state inputs (x=1 or x=0).
|
|
x=0 |
x=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
STEP 3:STATE REDUCTION.
Definition:
State
Si is equivalent to state Sj if and only if for every input combination:
- The output of Si is equivalent to the output of Sj
- The next state of Si is equivalent to the next state of Sj
- Reflexivity: Si = Si for any state.
- Symmetry: if Si = Sj then Sj = Si.
Transitivity: if Si = Sj and Sj = Sk, then we are quaranteed without even checking that Si = Sk (and, therefore, Si = Sj = Sk).
Reduction of completely
specified state tables:
Example 1: reduce
the state table
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) a = b if c =
d and b = b ==> a = b if c = d
(2) c = d if a =
b and c = d ==> c = d if a = b
From (1) and (2)
we can conclude that a = b and c = d.
The reduced state table:
A = {a,b}
B = {c,d}
| p.s. | x = 0 | x = 1 |
| A | B/0 | A/1 |
| B | A/1 | B/0 |
Example 2:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Implication table:
For example:---------- b (b,f) (d,h) x ----------------- c x x ------------------------ d (c,d) x x (e,f) eq ------------------------------ e (b,d) (d,f) (c,h) (c,d) x x x x -------------------------------------- f (b,c) (c,f) (c,d) (c,h) (c,d) x x eq x x ------------------------------------------------- g (b,c) (c,f) (c,d) (c,d) (d,h) x x x eq eq x ------------------------------------------------------- h (c,d) (a,f) x x (a,e) x x x x x -------------------------------------------------------- a b c d e f g
- c and f are not equivalent. (Writing x in their cell).
- g and b are equivalent iff c and f are identical. (we writh (c,f) in the gb cell). Cell cf contain x so we write x in gb.
Naming the sets: A = {a} B = {b} C = {c,d} D = {e,f,g} E = {h}
The reduced state table:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
example 3: Reduction in the division method:
At the beginning all the states are at the same equivalence class.Now we start to separate states which are not equivalent to the others.
F is not equivalent to the others:
x=0 x=1at the end:
-------------------------------
A1 B1/0 C1/0
B1 D1/0 E1/0
C1 G1 /0 E1/0
D1 H1/0 F2/0
E1 G1 /0 A1/0
F2 G1 /1 A1/0
G1 D1/0 C1/0
H1 H1/0 A1/0
x=0 x=1
-------------------------------
A1 B4/0 C1/0
B4 D3/0 E1/0
C1 G4 /0 E1/0
D3 H5/0 F2/0
E1 G4 /0 A1/0
F2 G4 /1 A1/0
G4 D3/0 C1/0
H5 H5/0 A1/0
The classes are:
a = (A,C,E) b = (B,G) c = (D)
d = (F) e = (H)
Step 4: Logical implementation. (detection overlapping sequence of 1111)
Determination of logical states
---------------------------------
0
0
0
0
0
0
0
0
1
0
1
0
0
1
0
0
0
0
0
1
1
1
0
0
1
0
0
0
0
0
1
0
1
1
1
0
1
1
0
0
0
0
1
1
1
1
1
1
The implementation:

Y0 = x y1 + x y0
= x ( y0 + y1)
Y1 = y1' x + y0
y1 x = x (y0 + y1')
z = y0 y1 x