Next: Complexity
Up: Spliced Alignment
Previous: Spliced alignment problem
Spliced alignment algorithm
To solve the problem,
we use dynamic programming.
We start with a few notations: Let
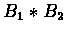 denote the concatenation of B1 and B2.
A j-prefix of
denote the concatenation of B1 and B2.
A j-prefix of
 is
is
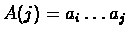 .
For block
.
For block
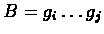 First(B) = i and
First(B) = i and
 .
A Chain
.
A Chain
 ends at
ends at
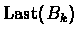 ,
and it ends
before position i, if
,
and it ends
before position i, if
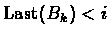 .
In addition, we define
.
In addition, we define
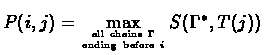 .
According to these definitions, the optimal spliced alignment score is P(n+1,m).
When First
.
According to these definitions, the optimal spliced alignment score is P(n+1,m).
When First
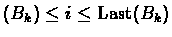 we can define the i-prefix of
we can define the i-prefix of
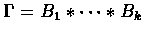 by the following expression:
by the following expression:
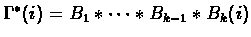 .
If First
.
If First
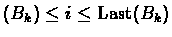 we define
we define
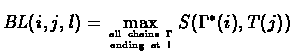 .
Now, we can calculate P(i,j) :
.
Now, we can calculate P(i,j) :
 .
.
 BL(i,j,l) satisfies the following recurrence
relation:
BL(i,j,l) satisfies the following recurrence
relation:
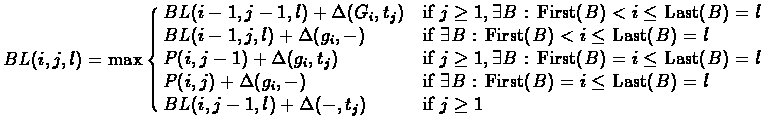
Itshack Pe`er
1999-02-03
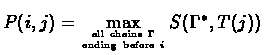 .
According to these definitions, the optimal spliced alignment score is P(n+1,m).
When First
.
According to these definitions, the optimal spliced alignment score is P(n+1,m).
When First
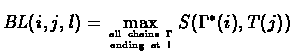 .
Now, we can calculate P(i,j) :
.
Now, we can calculate P(i,j) :  BL(i,j,l) satisfies the following recurrence
relation:
BL(i,j,l) satisfies the following recurrence
relation: