Definition 1

A Non Deterministic Büchi Automaton (NBA) is a 5-tuple: A = <Q, Σ, δ_A, q₀, F>, consisting of:

a finite set of states (Q)

a finite set of input symbols called the alphabet (Σ)

a transition function (δ_A : Q × Σ → 2^Q)

an initial or start state (q₀∈Q)

a set of accept states (F⊆Q)

Let w = a₁a₂ ... be an infinite string over the alphabet Σ. The automaton A accepts the string w if there exists a run π,π₁,π₂,... ∈ Q^ω with the following conditions:

π₀ = q₀

π_m+1 = δ_A(π_m, a_m) for all m ∈ {0, 1, 2, ...}

π_m ∈ F for infinitely many m's.

In words, the first condition says that the machine starts in the start state q₀. The second condition says that given each character of the string w, the machine will transition from state to state according to the transition function δ. The last condition says that the machine accepts w if the run never stops visiting accepting states. Otherwise, it is said that the automaton rejects the string. The set of strings that A accepts is the language recognized by A and this language is denoted by L(A).

Definition 2

A Deterministic Numbered Automaton (DNA) is a 6-tuple: D = <Q, Σ, δ_D, q₀, N, k>, consisting of:

a finite set of states (Q)

a finite set of input symbols called the alphabet (Σ)

a transition function (δ_D : Q × Σ → Q)

an initial or start state (q₀ ∈ Q)

a numbering function (N : Q × Σ → [k])

Let w = a₁a₂ ... be an infinite string over the alphabet Σ. The automaton A accepts the string w if there exists a run π,π₁,π₂,... ∈ Q^ω with the following conditions:

π₀ = q₀

π_m+1 = δ_A(π_m, a_m) for all m ∈ {0, 1, 2, ...}

min_i[N(π_m, a_m) = i for infinetle many m's] % 2 = 1

In words, the first condition says that the machine starts in the start state q₀. The second condition says that given each character of the string w, the machine will transition from state to state according to the transition function δ. The last condition says that the machine accepts w if the minimal numbering of the transitions which the run goes through infinitely is odd. Otherwise, it is said that that the automaton rejects the string. The set of strings that D accepts is the language recognized by D and this language is denoted by L(D).

Observe that the number associated with the transition leading to π_m is completely ignored by the transition function (that is, numbering is memoryless).

Note: this is a special case of the parity-acceptance condition for ω-automata in terms of expression. That is, one can associate the number assigned to the transition to the resulting state instead, multiply the number of states by k, and this will result in a parity automaton. This however could be more efficient in terms of the size of the resulting automaton as well as the complexity of deciding non-emptiness, which is only logarithmic in k.

Determinization Construction

Given an n-states Büchi automaton NBA A, the determinized NBA automaton D has states that are subsets' labeled trees, with n states.

Preliminaries

Trees

Let us represent an n-vertex tree by an n-dimensional vector. Each entry in the vector corresponds to a (not necessarily active) vertex in the tee, where the entry points to its parent:

Definition 3

An n-vertex tree T is a function T:{1,2,...n - 1} → {0, ..., n - 2} such that T[u] < u for all 1 ≤ u ≤ n - 1. T[u] is referred to as u's parent. A parent's index is always smaller than its children's.

This function is interpreted as a tree in which 0 is the root, and each vertex represented at entry u, has T[u] pointing to its parent entry.

Let us denote by T_n the set of all such trees (vectors). Clearly, since T[u] can take up to u values, the number of such tress is at most (n - 1)!.

The following terminology will be used throughout this paper:

T*[u] is the set of ancestors of u, namely: T*[u] =^def { T^j[u] | j > 0 }

u is a child of v if T[u] = v.

u is a senior sibling of v if T[v] = T[u] and u < v.

u is a descendant of v if T*[u] = v.

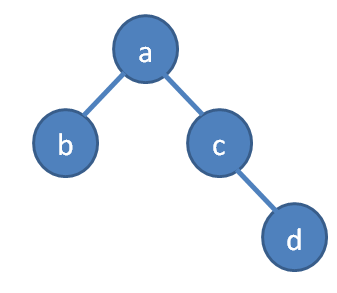
the tree above can be represented as: [0,0,2], when b is a senior sibling of c.

Subsets' Labeling

Let us now extend trees into labeled trees, in which vertices are labeled by subsets of states {1, ..., n}. The subsets' labeling of the tree combined with the tree itself must satisfy properties which will be specified momentarily. The actual representation of the labeling could consequently be represented quite efficiently as will be specified below.

Definition 4

Assume an NBA A with set of states Q. A pair comprising a tree T ⊆ T_n and a labeling S of subset of Q to every vertex u of T is called proper if it satisfies the following properties:

Hereditary: the label of a vertex u is a subset of the label of its parent T[u]:
∀u, S[u] ∈ S[T[u]]

Unique: every vertex has a state in its label, which does not occur in any of its decendants' labels:
∀u, S[u] ≠ ∪_{v: T[v]
= u} S[v]
In other words, taking hereditary into account, the above says that the union of all u's descendants' labels is proper subset of u's label.

Partition: children's labels are pairwise non-intersecting:
∀u,v s.t. T[u] = T[v] : S[u] ∩ S[v] = ∅

Packed: there is a 1 ≤ t ≤ n so that all vertices u > t are labeled by the empty set S[u] = ∅ and T[u] = 0 (namely, inactive vertices arbitrarily point to the root as their parent), and all u ≤ t are labeled by a non-empty set.

It is hence possible to specify for each state, the highest indexed vertex u in the tree in whose labeling it appears. The following definition captures the fact that if a pair
(T, S) is proper, then S can be represented efficiently.

Definition 5

A Q-labeling of a tree T ∈ T_n is a partial function s: Q → {0, ..., n - 1} which maps a (reachable) state q to a vertex in the tree T. s is proper if there is a 0 ≤ t ≤ n so that every vertex u ≤ t is assigned its (unique) state, namely s^-1[u] is defined, while no vertex u > t is assigned a state (and its parent is 0). t is then referred to as the actual size of the tree T.

The subset S[u] associated with a vertex u is the set of states that are assigned to any of its descendants:

S[u] =^def { q | s[q] = v, u ∈ T*[v] ∨ u = v }

Let us denote the set of proper Q-labeling by L_n. Combined, the tree and the labeling specify a labeled tree:

Definition 6

An n-subsets-labeled tree is a pair (T, s) ∈ T_n × L_n, where s is proper.

Determinization of an ω-automaton with n states

Given an NBA A with n states, A = <{1, ..., n} Σ δ_A, 1, F>, the states of the DNA D are:

Q =^def T_n × L_n

namely

Q =^def {(T, s)| T is an n-vertex tree, s is a proper labeling }

Initial State

D's initial state is the tree that has only the root. The set {1} (the singleton of the initial state of A) is the label at the root so s[1] = 0, and t = 0. Namely, s is undefined for all other states and T[u] = 0 for all u.

The Transition Function

Given a state q ∈ Q and a letter a ∈ Σ, one has to describe the outcome state δ_D(q, a) of the deterministic automaton, plus the number N(q, a) by which the transition is labeled. This will be carried out via a few steps and a few intermediate constructs. One starts with a state q = (T, s) and constructs δ_D((T, s), a) = (T''', s''') and N((T, s), a) = l for any letter a read.

Spawning

For every vertex u in T, apply A's transition relation δ_A to obtain

S'[u] =^def
δ_A(S[u], a) =
∪_{q' ∈ S[u]} δ_A(q', a)

for the letter a ∈ Σ.

Then, for every vertex u add a vertex to the tree at n + u and label it by the subset S'[u] ∩ F. The parent of this new vertex is u, namely, T'[n + u] =^def = u. The outcome is
T' ∈ T_2n and the labeling S'[u], which assigns subsets to vertices of T'. Note that the pair does not necessarily satisfy many of the properties that need to be kept. For starters, there are too many vertices in the tree. Clearly, the hereditary property still holds. However, the uniqueness and partition conditions are not necessarily maintained. This will be fixed by the next couple of adjustments presented next.

for example, for the tree the transition function:

and the tree:

which is actually the following tree (since n = 2):

the result of spawning will be:

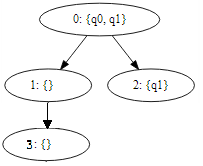
Seniority Rules

The goal of this adjustment is to restore the partition condition. Simply put, when having two siblings share a state in their labeling, only the senior of them gets to keep it. Formally, the new labeling S'' is defined as follows. For every vertex u in the tree,

S''[u] = S'[u] \ ∪_{v
< u: T[v] = T[u]} S'[v]

∪_{v < u: T[v] =
T[u]} S'[v] is also removed from all of u's descendants in order to retain hereditary.

In other words, s'' assigns to every reachable state q the one vertex whose children's labeling do not contain it at the end of a recursive search, where one always chooses the most senior (smallest indexed) child whose label contains q.

Claim 0.1

S'' has the partition property. Namely, if u, v are siblings then S''[u] ∩ S''[u] = ∅.

for example the following tree:

will look like this after applying seniority rules:

note that this tree does not have the uniueness property.

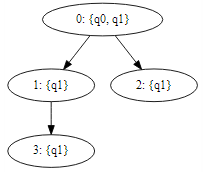
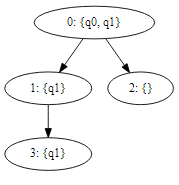
Restoring the Uniqueness property

For any vertex u in T, if the union of subsets of its descendant equals u's, namely

S''[u] = S'[u] \ ∪_{v:
T[v] = u} S''[v]

Then, eliminate all of u's descendants and adjust state-labeling accordingly (namely, let s[q] of all states q so that s''[q] is a descendants to u). Denote by g the smallest index of a vertex u whose descendants are eliminated (infinity if none).

Claim 0.2

S'' has the uniqueness property.

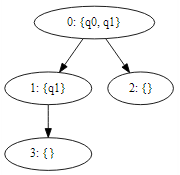
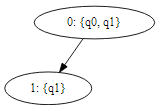
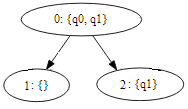
After applying this step on the tree in D7, it should look like this:

the unique state of node 0 is q0 and the unique state of node 1 is q1.
since nodes 2 and node 3 has no unique state, the tree is equivalent to:

Packing the Tree

Some of the vertices may so be eliminated. Assign to every vertex u, the entry u' which is its order among non eliminated vertices. Adjust pointers and labeling accordingly.

This restores all properties of the original tree: there is some t' so all vertices up to there are alive each such vertex has some state i, so that s'[i] = u therefore, there are at most n vertices to the tree.

For example, the following tree:

will look like this after packing:

D10

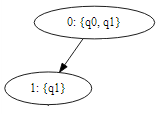
Let b be the index of the first eliminated vertex. Namely, all vertices u < b have stayed intact. The number assigned to the new state is calculated as follows: Let k be the minimum between g and b. The number is 2k if b is not larger than g, and 2k + 1 otherwise.

This ends the description of the transition function, and thus the construction.

Proof of Correctness

Claim 0.3

At any time m (that is, the state reached by the automaton after reading a₁, ..., a_m) the subset S' is exactly the reachable states in A at time m.

Soundness

Let us first prove that if a string w ∈ Σ ^ω is accepted by D, then w is accepted by A.

Let us denote the smallest number that occurs infinitely many times as 2b + 1. Then, past some prefix of the word, all first b vertices stay intact. Moreover, the b'th vertex, for infinitely many times, becomes green, and is left without children, as S'[b] is the same as the union of its descendants: g = b infinitely often. Let m₀ be the first such time that g = b past the prefix, m₁ the second, and so on.

Now, between any m_i and m_{i + 1} all states in S[b] at time m_{i + 1} have run segments, over a_{m_i + 1}, ..., a_{m_{i +
1}} , which stem from the label S[b] at m_i and have visited an accepting state in F in between. By Konig's lemma, this implies that there is a run that visits the accepting set infinitely many times.

Completeness

Now, let us prove that if w is accepted by A then it is accepted by D.

Given an accepting run, π ∈ [n]^ω of A on w ∈ Σ^ω, let us follow closely the state π _m of A and which labels it is in, on the sequence of states (T_m, s_m) of the run of D on w.

Observe that π_m S[0], the labeling of the root 0 induced by the state (T_m, s_m), for all m.

If 1 occurs infinitely many times (namely, the root is green infinitely often), D accepts w and we are done.

Otherwise, let m₀ be the largest in which g = 0, and m'₀ > m₀ be the first so that π_m'₀ ∈ F. At m'₀ there must be a child of vertex 0 that contains π_m'₀, π_m for m > m'₀ is always in one of vertex 0's children and can shift children, however always to a more senior one (and may also shift for the tree to be packed). But all these can only happen finitely many times.

Let m₁ be the last time when such a shift occurs, and u be the vertex where the π's state reside from then on.

Proceed recursively for u beyond m₁:

No even numbers ≤ 2b occur beyond that point; if u is green infinitely many times, thus 2b + 1 occurs infinitely often, we are done.

If not, there must be a time m'₁ after which the state π_m occurs in a child of u...

Since the depth of the tree is finite, the recursion must end with an odd number occurring infinitely many times, and no smaller number occurs more than finitely many times. ∎

Determinization Construction: NBA ↬ DNA

Motivation

ω-Automata