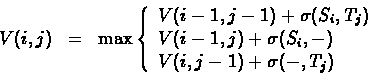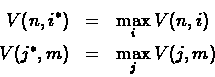Motivation

One example where end-spaces should be free is in the shotgun sequence assembly procedure. In this problem, one has a large set of partially overlapping substrings that come from many copies of one original but unknown DNA sequences. The problem is to use comparisons of pairs of substrings to infer the correct original string. Two random substrings from the set are unlikely to have nearby starting positions in the original string, and this is reflected by a low end-space free alignment score for those two substrings. But if two substrings do overlap in the original string, then an alignment may be between suffix of one to a prefix of the other with only a small number of spaces and mismatches. This overlap is detected by an end-space free weighted alignment with high score. 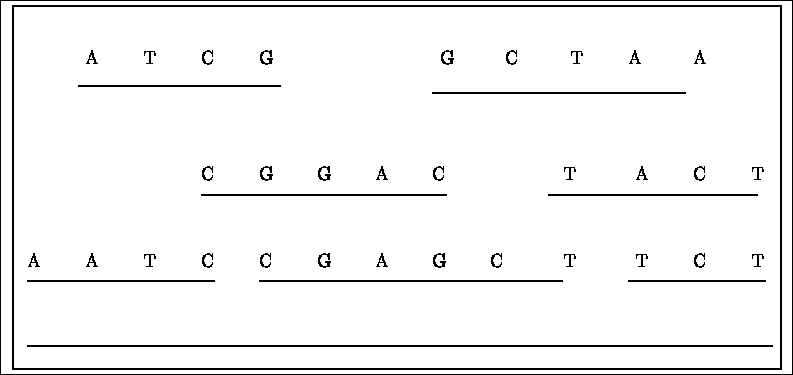Similarly, the case when one substring contains another can be detected in this way. See figure 2.4 for illustration.

  

Figure 2.4: sequence assembly

When comparing two strings, it is not obvious how to place the two strings, so that the similarity between the two will be maximal. One possibility, denoted by the ends free problem is to disregard leading and trailing indel operations (in the usual similarity strategy, all indel operations reduce the similarity).

To implement this we will change the algorithm presented for the global alignment problem, as follows:

• Set initial conditions:
  
  $$\begin{eqnarray*}V(i, 0) &=& 0 \hspace{2cm}{\rm for\;} 1 \le i \leq n\\ V(0, j) &=& 0 \hspace{2cm}{\rm for\;}1 \le j \leq m \end{eqnarray*}$$
  
  
• Use the same recurrence for ${1 \leq i \leq n}$, ${1 \leq j \leq m}$
  
  $$\begin{eqnarray*}V(i,j) &=& \max \left\{\begin{array}{lll} V(i-1,j-1)+\sigma(S_... ...igma(S_i, - )\\ V(i ,j-1)+\sigma( - ,T_j) \end{array} \right. \end{eqnarray*}$$
  
  
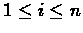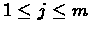
• Instead for looking at V(n, m) the algorithm will search for i^* and j^* so that:
  
  $$\begin{eqnarray*}V(n, i^{*}) &=& \max_{i} V(n,i)\\ V(j^{*}, m) &=& \max_{j} V(j, m) \end{eqnarray*}$$
  
  
• The similarity will be defined as:
  
  $$\begin{eqnarray*}V(S, T) &=& \max \{ V(n, i^{*}), V(j^{*}, m) \} \end{eqnarray*}$$
  
  

Looking for i^* means searching for a cell in the last row of the table, produced while computing V(n,m). Looking for j^* means searching for a cell in the last column of the same table. This eliminates trailing indel operations. Leading indel operations will not be taken into account due to the changes in the initial conditions.

Complexity :

• Time complexity - Computing the matrix takes O(nm). Finding j^* and i^* takes O(n+m). Therefore the total complexity remains O(nm).

• Space complexity - Computing the matrix takes O(n + m) space. Computing the maximizing values i^*, j^* requires the last row and column to be saved, which is also O(n + m). Therefore the total complexity remains O(n + m).