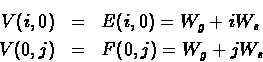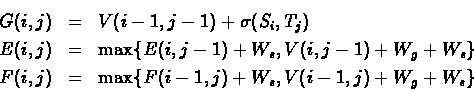Next: Longest Common Subsequence
Up: Gap Penalty
Previous: Constant gap weight model
Affine gaps penalty
To align strings S, T, consider as usual the prefixes
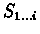 of S and
of S and
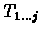 of T. Any alignment of these two prefixes is one of the following three types:
of T. Any alignment of these two prefixes is one of the following three types:
- 1.
- S ------i
T ------j
alignment of
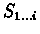 and
and
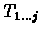 where characters S(i) and T(j) are aligned opposite each other. This includes
both the case that
Si = Tj and that
where characters S(i) and T(j) are aligned opposite each other. This includes
both the case that
Si = Tj and that
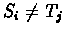 .
.
- 2.
- S ------i_ _ _ _ _ _ _
T -------------j
alignment of
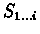 and
and
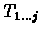 where character Si is aligned to a character strictly to the left of character Tj.
Therefore, the alignment ends with a gap in S.
where character Si is aligned to a character strictly to the left of character Tj.
Therefore, the alignment ends with a gap in S.
- 3.
- S --------------i
T ------j_ _ _ _ _ _ _ _
alignment of
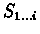 and
and
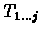 where character Si is aligned to a character strickly to the right of character Tj. Therefore, the alignment ends with a gap in T.
where character Si is aligned to a character strickly to the right of character Tj. Therefore, the alignment ends with a gap in T.

Hence the base conditions are:
and the recursive computation of V(i, j) will be:
while
The optimal value alignment is the maximum value in the nth row or m column.
Complexity
- Time complexity - As before O(nm), as we only compute four matrices instead of one.
- Space complexity - There's a need to save four matrices (for E, F, G, and V respectively) during the computation. Hence, O(nm) space is needed, for the trivial implementation.



Next: Longest Common Subsequence
Up: Gap Penalty
Previous: Constant gap weight model
Itshack Pe`er
1999-01-03
![]() of S and
of S and
![]() of T. Any alignment of these two prefixes is one of the following three types:
of T. Any alignment of these two prefixes is one of the following three types:
![]() and
and
![]() where character Si is aligned to a character strictly to the left of character Tj.
Therefore, the alignment ends with a gap in S.
where character Si is aligned to a character strictly to the left of character Tj.
Therefore, the alignment ends with a gap in S.
![]() and
and
![]() where character Si is aligned to a character strickly to the right of character Tj. Therefore, the alignment ends with a gap in T.
where character Si is aligned to a character strickly to the right of character Tj. Therefore, the alignment ends with a gap in T.