Longest Common Subsequence

Next: Polymerase Chain Reaction Up: Pairwise Alignment Previous: Affine gaps penalty

Longest Common Subsequence

$\begin{dfn}{\rm {\em Subsequence} is defined as a subset of the characters of st... ...y this list of indices is the string $S_{i_1}S_{i_2}\ldots S_{i_k}$ .} \end{dfn}$

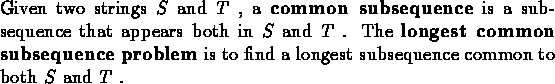
$\begin{dfn}{\rm Given two strings $S$\space and $T$ , a {\bf common subsequence}... ...} is to find a longest subsequence common to both $S$\space and $T$ .} \end{dfn}$

The problem of Longest Common Subsequence can be modeled and solved using the optimal alignment algorithm with the following scoring:

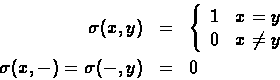
$\begin{eqnarray*}\sigma(x,y) &=& \left\{\begin{array}{ll} 1 & x=y\\ 0 & x\neq y \end{array} \right. \\ \sigma(x,-) = \sigma(-,y) &=& 0 \end{eqnarray*}$

Or, directly compute V(n, m) with:

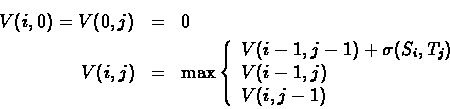
$\begin{eqnarray*}V(i,0)=V(0,j)&=&0\\ V(i,j) &=& \max \left\{\begin{array}{lll} ... ...+\sigma(S_i,T_j)\\ V(i-1,j)\\ V(i ,j-1) \end{array} \right. \end{eqnarray*}$

Each character in the string S can be align with the same character in the string T or with a space in T (in this case no substitution is done). Since the goal is to find maximum length, character matched are valued as '1', while a space match is valued '0'.

Itshack Pe`er
1999-01-03