INPUT: A set of sequences
QUESTION: Compute a global multiple alignment
Proof:Since the triangle inequality holds for every single column of the alignment by the definition of the scoring scheme, it also holds for entire strings by the definition of d. Therefore
Let
![]() denote the optimal alignment of
denote the optimal alignment of ![]() .
Let
d*(Si,
Sj) denote the value of alignment between Si and Sj induced
by
.
Let
d*(Si,
Sj) denote the value of alignment between Si and Sj induced
by
![]() .
.
Proof:By Lemma 5.2 it follows that
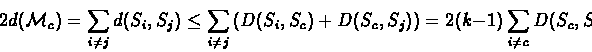 |
(5.1) |
| (5.2) |
| (5.3) |
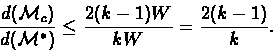 |
(5.4) |