Forward and Backward Probabilities for a Profile HMM

In the previous section we modeled the problem of aligning a string to a profile. As with general HMMs, the main problem is to assign meaningful values to the transition and emission probabilities to a profile HMM. It is possible to use the Baum-Welch algorithm for training the model probabilities, but it remains to show how to compute the forward and backward probabilities needed for the algorithm.
Given a string 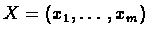$X=(x_{1},\ldots,x_{m})$ we define:

• The forward probabilities:
  

  $$f^{M}_{j}(i) = P(x_{1},\ldots,x_{i} \,\text{ ending at } M_{j})$$ (6.46)

  $$f^{I}_{j}(i) = P(x_{1},\ldots,x_{i} \,\text{ ending at } I_{j})$$ (6.47)

  $$f^{D}_{j}(i) = P(x_{1},\ldots,x_{i} \,\text{ ending at } D_{j})$$ (6.48)

  
  

• The backward probabilities:
  

  $$b^{M}_{j}(i) = P(x_{i+1},\ldots,x_{m} \,\text{ beginning from } M_{j})$$ (6.49)

  $$b^{I}_{j}(i) = P(x_{i+1},\ldots,x_{m} \,\text{ beginning from } I_{j})$$ (6.50)

  $$b^{D}_{j}(i) = P(x_{i+1},\ldots,x_{m} \,\text{ beginning from } D_{j})$$ (6.51)

  
  

Computing the Forward Probabilities:

1.

Initialization:

f_begin(0) = 1 (6.52)

2.

Recursion:

$$\begin{split} f_{j}^{M}(i) = e_{M_{j}}(x_{i}) \, \cdot \, ... ...\ &f^{D}_{j-1}(i-1)\cdot a_{D_{j-1},M_{j}}] \end{split}$$ (6.53)

$$\begin{split} f^{I}_{j}(i) = e_{I_{j}}(x_{i}) \, \cdot \, ... ...}}+\\ &f^{D}_{j}(i-1)\cdot a_{D_{j},I_{j}}] \end{split}$$ (6.54)

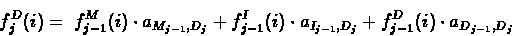$$\begin{split} f^{D}_{j}(i) = \; &f^{M}_{j-1}(i)\cdot a_{M_{... ...}+\\ &f^{D}_{j-1}(i)\cdot a_{D_{j-1},D_{j}} \end{split}$$ (6.55)

Computing the Backward Probabilities:

1.

Initialization:

b^M_L(m) = a_ML,end (6.56)

b^I_L(m) = a_IL,end (6.57)

b^D_L(m) = a_DL,end (6.58)

2.

Recursion:

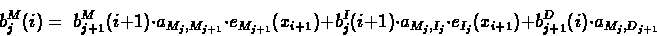$$\begin{split} b_{j}^{M}(i) = \; &b^{M}_{j+1}(i+1)\cdot a_{M... ...+ \\ &b^{D}_{j+1}(i)\cdot a_{M_{j},D_{j+1}} \end{split}$$ (6.59)

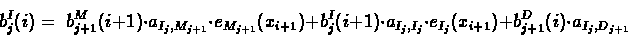$$\begin{split} b^{I}_{j}(i) = \; &b^{M}_{j+1}(i+1)\cdot a_{I... ...)+\\ &b^{D}_{j+1}(i)\cdot a_{I_{j},D_{j+1}} \end{split}$$ (6.60)

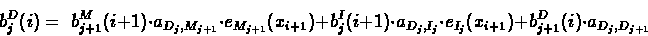$$\begin{split} b^{D}_{j}(i) = \; &b^{M}_{j+1}(i+1)\cdot a_{D... ...)+\\ &b^{D}_{j+1}(i)\cdot a_{D_{j},D_{j+1}} \end{split}$$ (6.61)