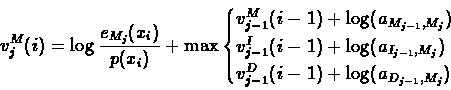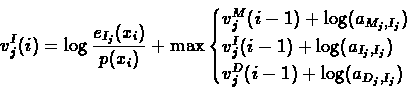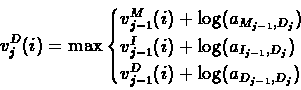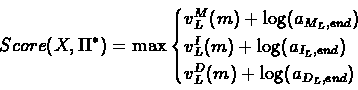Next: Forward and Backward Probabilities
Up: Profile Alignment
Previous: Profile HMMs
Aligning Sequences to a Profile HMM
To align the string
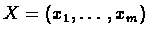 against a profile
against a profile
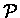 of length L, we will use a variant of the Viterbi
algorithm. For each
of length L, we will use a variant of the Viterbi
algorithm. For each
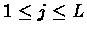 and
and
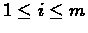 we use
the following definitions:
we use
the following definitions:
- Let
vMj(i) be the logarithmic likelihood score of the best
path for matching
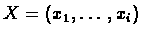 to the profile HMM
to the profile HMM
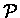 ,
ending with xi emitted by the state
Mj.
,
ending with xi emitted by the state
Mj.
- Let
vIj(i) be the logarithmic likelihood score of the best
path for matching
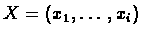 to the profile HMM
to the profile HMM
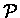 ,
ending with xi emitted by the state
Ij.
,
ending with xi emitted by the state
Ij.
- Let
vDj(i) be the logarithmic likelihood score of the best
path for matching
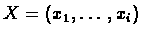 to the profile HMM
to the profile HMM
 ,
ending with the state Dj (without emitting any symbol).
,
ending with the state Dj (without emitting any symbol).
The initial value of the special begin state is:
To calculate the values of
vMj(i),
vIj(i) and
vDj(i) we use the same technique as in the Viterbi
algorithm. There are however two major differences:
- Each state in the model has at most three entering
links (see figure 6.5).
- The deletion states are silent - they cannot emit any
symbol.
The three predecessors of the match state Mj are the three
states of the previous layer, j-1:
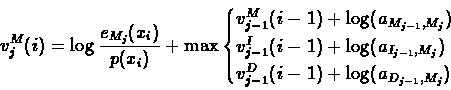 |
(6.42) |
The three predecessors of the insertion state Ij are the
three states of the same layer, j:
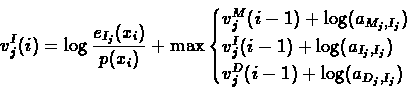 |
(6.43) |
The three predecessors of the deletion state Dj are the three
states of the layer j-1. Since Dj is a silent state, we
should not consider the emission likelihood score for xi in
this case:
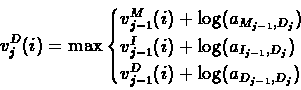 |
(6.44) |
We conclude by calculating the optimal score:
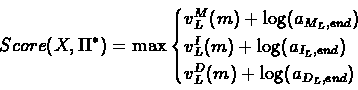 |
(6.45) |
Complexity: We have to calculate
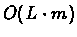 values,
while calculating each value takes O(1) operations (since we
only need to consider the scores at most three predecessors). We
therefore need
values,
while calculating each value takes O(1) operations (since we
only need to consider the scores at most three predecessors). We
therefore need
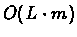 time and
time and
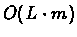 space.
space.
Figure 6.6:
Profile
HMM for local alignment
|
|
We can use a similar approach for the problem of local alignment
of a sequence versus a profile HMM. This is achieved by adding
four additional states (the lightly shaded states in figure
6.6) corresponding to the alignment
of a sub-string of X to a part of the profile.



Next: Forward and Backward Probabilities
Up: Profile Alignment
Previous: Profile HMMs
Itshack Pe`er
1999-01-24