


Next: Least Squares Methods
Up: Distance Matrix Methods
Previous: Distance between Proteins -
Distance between DNA Sequences - Jukes-Cantor Model
According to the model of Jukes and Cantor [8] each base in the DNA
sequence has an equal chance of mutating, and when it does, it is replaced by some
other nucleotide uniformly. For a mutation probability of
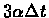 during each infinitesimally small period of time
during each infinitesimally small period of time 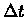 ,
the chance of a
nucleotide x remaining unchanged over a period of T time units is (recall
exercise #1):
,
the chance of a
nucleotide x remaining unchanged over a period of T time units is (recall
exercise #1):
Given a branch in the tree, the probability that the site is different at the two
edges is therefore:
The Jukes-Cantor model defines an additive distance by using the difference per
site to estimate
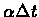 itself. The values of
itself. The values of
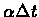 on each
branch will, by definition, add perfectly.
on each
branch will, by definition, add perfectly.
Itshack Pe`er
1999-02-18