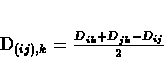Next: Maximum Likelihood
Up: Distance Matrix Methods
Previous: UPGMA
Neighbor Joining
The Neighbor-Joining algorithm is another quick clustering technique, which
attempts to approximate the least squares tree, this time without resorting to the
assumption of a molecular clock. The idea here is to join clusters
that are not only close to one another, but are also far from the rest.
In each iteration, the algorithm attempts to find the direct ancestor of two sepcies
in the tree. For node i, its distance ui from the rest of the tree is
estimated using the formula:
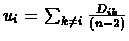 .
In order to
minimize the sum of all branch lengths, also known as the minimum-evolution criterion,
the nodes i and j that are clustered next are those for which
Dij - ui - uj is
smallest (the reader is reffered to [9] for a more elaborate explanation on this
issue). The lengths
dk,(ij) of the new branches are calculated by solving the same
system of linear equations mentioned earlier in section 9.4.1.
The solutions are written below, in equations 9.8 and
9.9.
Neighbor-Joining has a running time of O(n2), like UPGMA.
.
In order to
minimize the sum of all branch lengths, also known as the minimum-evolution criterion,
the nodes i and j that are clustered next are those for which
Dij - ui - uj is
smallest (the reader is reffered to [9] for a more elaborate explanation on this
issue). The lengths
dk,(ij) of the new branches are calculated by solving the same
system of linear equations mentioned earlier in section 9.4.1.
The solutions are written below, in equations 9.8 and
9.9.
Neighbor-Joining has a running time of O(n2), like UPGMA.
Neighbor-Joining algorithm [11]:
- Initialization: same as in UPGMA (see 9.4.5).
- Iteration:
- 1.
- For each species, compute
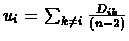 .
.
- 2.
- Choose the i and j for which
Dij - ui - uj is smallest.
- 3.
- Join clusters i and j to a new cluster - (ij), with a corresponding
node in T. Calculate the branch lengths from i and j to the new node as:
 |
(9.7) |
- 4.
- Compute the distances between the new cluster and each other cluster:
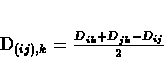 |
(9.8) |
- 5.
- Delete clusters i and j from the tables, and replace them by (ij).
- 6.
- If more than two nodes (clusters) remain, go back to
1. Otherwise, connect the two remaining nodes by a
branch of length Dij.
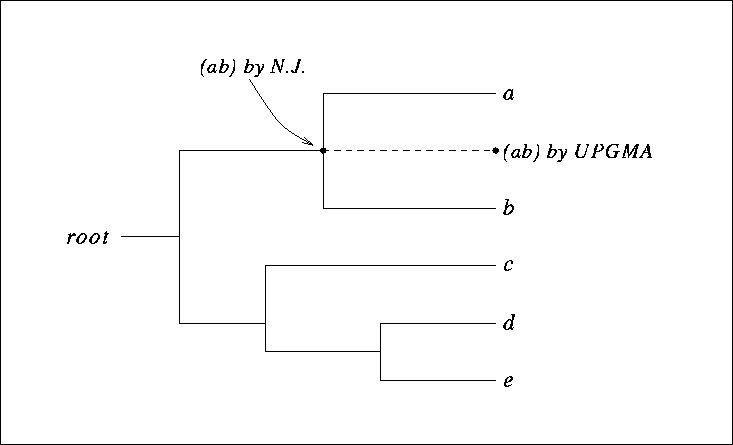
Figure 9.9:
A clocklike tree, showing the clustering (ab) of the two nodes a and b by UPGMA and by the Neighbor-Joining algorithm.
|
|



Next: Maximum Likelihood
Up: Distance Matrix Methods
Previous: UPGMA
Itshack Pe`er
1999-02-18
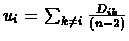 .
.