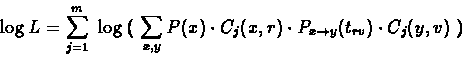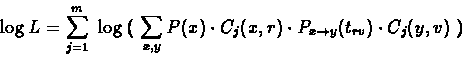Next: Bibliography
Up: Maximum Likelihood
Previous: Computing the Likelihood of
Finding the Optimal Branch Lengths
We are now ready to tackle the more difficult task of finding the optimal branch
lengths for a given tree topology. First, let us assume that all the lengths are
known except for trv. If r is the root (as in figure
9.10), then we get:
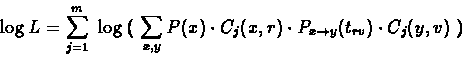 |
(9.14) |
which is an elementary function of trv and some constants.
We now need to maximize 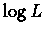 with respect to trv. This can be done by many
standard methods, e.g., Newton-Raphson, or EM algorithm. The same process we have
just demonstrated can also be applied when r is not the original root. As
explained earlier, if
with respect to trv. This can be done by many
standard methods, e.g., Newton-Raphson, or EM algorithm. The same process we have
just demonstrated can also be applied when r is not the original root. As
explained earlier, if
 for any
x, y, and t, then the root can be set at any node, without affecting L. In
other words, in order to find an optimal branch length between nodes r and v,
we simply need to hang the tree from r, so that the previous analysis holds.
Our next step is to find optimal branch lengths, when none of them are known
apriori. The main problem is that once one branch has changed length, there is no
guarantee that the others are still at their optimal lengths. On the contrary, the
branches are clearly not pairwise independent. In practice, however, locally improving the
likelihood by optimizing the length of one branch at a time works quite well, as there are
not very strong interactions between branch lengths. After a few sweeps through the tree,
calculating the optimal length of each edge separately, the likelihood converges,
and the result is a near-optimal phylogenetic tree.
for any
x, y, and t, then the root can be set at any node, without affecting L. In
other words, in order to find an optimal branch length between nodes r and v,
we simply need to hang the tree from r, so that the previous analysis holds.
Our next step is to find optimal branch lengths, when none of them are known
apriori. The main problem is that once one branch has changed length, there is no
guarantee that the others are still at their optimal lengths. On the contrary, the
branches are clearly not pairwise independent. In practice, however, locally improving the
likelihood by optimizing the length of one branch at a time works quite well, as there are
not very strong interactions between branch lengths. After a few sweeps through the tree,
calculating the optimal length of each edge separately, the likelihood converges,
and the result is a near-optimal phylogenetic tree.



Next: Bibliography
Up: Maximum Likelihood
Previous: Computing the Likelihood of
Itshack Pe`er
1999-02-18