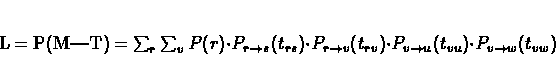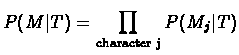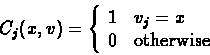Next: Finding the Optimal Branch
Up: Maximum Likelihood
Previous: Maximum Likelihood
Computing the Likelihood of a Tree
For the analysis below, we shall use the following terms:

. A reconstruction is a full
labeling of the tree's internal nodes. A branch length tvu is the
length of the edge between nodes v and u, and it measures the biological time,
or genetic distance, between the species associated with these nodes.
As always, we assume that the characters are pairwise independent, and that the
branching is a Markov process, that is, the probability of a node having a given
label is a function only of the state of the parent node and the branch length,
t, between them. Our model also includes a distance function to compute the
latter probability, i.e.:
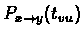 ,
the probability that
state x will transform into state y within the time tvu. We further assume
that the character frequencies are fixed throughout the evolutionary history, and
that they are given as P(x).
,
the probability that
state x will transform into state y within the time tvu. We further assume
that the character frequencies are fixed throughout the evolutionary history, and
that they are given as P(x).
Problem 9.11
Likelihood of a Tree.
INPUT:
- A matrix M describing a set of m characters for each one of n given
species.
- A tree T with the above species as its leaves and with known branch
lengths tvu.
QUESTION: Calculate the likelihood
L of the tree:
L =
P(
M|
T).
First, let us deal with a simple case, where there is only one character
identifying each species. Since the labels of the internal nodes are unknown, we
need to sum over all possible reconstructions. For example, for the tree
illustrated in figure 9.10, we can immediately write down the
following formula:
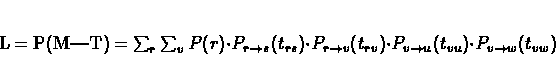 |
(9.9) |
where r and v are possible labels (character values) for the
corresponding nodes.
Figure 9.10:
A simple tree with branch lengths. The likelihood of this tree is calculated in equation 9.10.
|
|
To expand the formula for multiple characters, we simply need to repeat the above
calculation for each character separately, and then multiply the results (recall
the assumption that the characters are pairwise independent). The general equation
is now:
Note: The trees inferred by maximum likelihood appear from this
description to be rooted trees. However, if the model of character substitution is
reversible, i.e.,
 ,
then the tree
is actually unrooted - the root can be chosen arbitrarily, without any change in
the likelihood of the tree.
It now remains to show how this calculation can be performed efficiently. The
following dynamic-programming ``pruning'' algorithm was introduced by Felsenstein
[3].
,
then the tree
is actually unrooted - the root can be chosen arbitrarily, without any change in
the likelihood of the tree.
It now remains to show how this calculation can be performed efficiently. The
following dynamic-programming ``pruning'' algorithm was introduced by Felsenstein
[3].
Calculating the likelihood of a tree using Dynamic Programming:
For a character j, denote:
Cj(x,v) is the conditional likelihood of v's subtree, i.e., the probability
of everything that is observed from node v on the tree down to the leaves, at
character position j, given that v has the label x at this position.
- Initialization:
For each leaf v and state x:
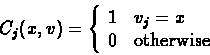 |
(9.11) |
- Recursion:
Traverse the tree in postorder; for an internal node v with children u and
w, compute for each possible state x:
 |
(9.12) |
- The final solution is:
 |
(9.13) |
Complexity: For n species, m characters, and k possible
states for each character, we perform
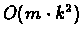 work in O(n) nodes, so
the running time of the algorithm is
work in O(n) nodes, so
the running time of the algorithm is
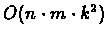 .
.



Next: Finding the Optimal Branch
Up: Maximum Likelihood
Previous: Maximum Likelihood
Itshack Pe`er
1999-02-18