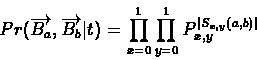Next: Problem Statement
Up: Constructing Physical Maps from
Previous: The Statistical Model
Clone Pair Overlap Score
Let Ca and Cb be two clones viewed as intervals of
lengths la and lb respectively. Without loss of
generality, assume
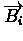 .
Define
.
Define
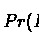 =
=
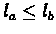 and
and
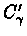 .
The
overlap score uses the hybridization vectors
.
The
overlap score uses the hybridization vectors
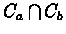 to produce a
vector probabilities for the overlap length
to produce a
vector probabilities for the overlap length
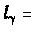 .
.
Figure 10.10:
Clone pair overlap
score
|
|
The relative position of Ca,Cb and
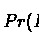 is
shown in figure 10.10.
We first calculate the probability
is
shown in figure 10.10.
We first calculate the probability
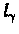 .
Let
.
Let
 ,
,
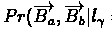 ,
and let
Ai,j be the number of occurrences of probe j in Ci. We
can thus write the following equation:
,
and let
Ai,j be the number of occurrences of probe j in Ci. We
can thus write the following equation:
The calculation of the probabilities inside the summation is
straightforward using the statistical model. Since hybridization
is a virtual certainty if a probe occurs many times inside a
clone, we can limit the summation to small values of k (say
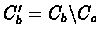 ), thereby making feasible the score's computation
while introducing only a negligible error. Considering each probe
as an independent source of information, the conditional
probability of the vector pair
), thereby making feasible the score's computation
while introducing only a negligible error. Considering each probe
as an independent source of information, the conditional
probability of the vector pair
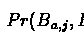 is:
is:
 |
(10.15) |
Assuming uniform parameters for the probes, the expression
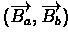 inside the product is
independent of j. Therefore, we can define
Px,yt by
Px,yt = Pr(Ba,j = x, Bb,j = y | t). Denoting by
Sx,y(a,b) the set of probes
inside the product is
independent of j. Therefore, we can define
Px,yt by
Px,yt = Pr(Ba,j = x, Bb,j = y | t). Denoting by
Sx,y(a,b) the set of probes
 ,
such that
Ba,j = x and
Bb,j = y, we can write:
,
such that
Ba,j = x and
Bb,j = y, we can write:
 |
(10.16) |
Having computed
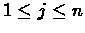 we can use Bayes Theorem:
we can use Bayes Theorem:
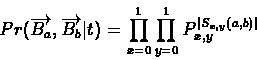 |
(10.17) |



Next: Problem Statement
Up: Constructing Physical Maps from
Previous: The Statistical Model
Itshack Pe`er
1999-03-21
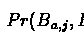 is:
is:
 ,
such that
Ba,j = x and
Bb,j = y, we can write:
,
such that
Ba,j = x and
Bb,j = y, we can write: