Results on Real DNA

The next step of the authors was to test the algorithm in simulations involving real DNA sequences. These sequences were taken from a variety of representative organisms: the nematode C. Elegans, bacterium E. Coli, yeast, and human. The lengths of the sequences ranged from about 1.7MB to over 4MB. Non overlapping sections of length 1MB from each genome were used for the tests (1MB and 730MB for Homo Sapiens). An additional random DNA sequence was used for comparison. With the exception of probes fitting repetitive sequences, the occurrences of most probes along target genome appear to be uniformly distributed (assumption 3 in section 10.3.2), thus supporting the Poisson model. However, the same rate assumption also predicts a Poisson distribution of the number of probe occurrences. As figure 10.14 demonstrates, this stronger assumption cannot be sustained. The obvious solution of fitting a separate Poisson model for each probe will not do, because most probes occur very infrequently, and will therefore provide very little information. However, Figure 10.14 leads us to an encouraging observation: In all the distributions, a significant fraction falls under the graph of the random DNA, thereby demonstrating that there are fairly many "good" probes. Because probe hybridizations are effort and cost intensive it is impractical to make a large amount of experiments and then choose a small subset of "good" probes. However, if probes can be chosen before the actual experiment, based on prior knowledge of the organism's typical sequences (e.g., from other sequenced parts of its genome), better results can be achieved. This process is called probe pre­selection. Figure 10.15 demonstrates that a fairly good fit with the same ­ rate model can be achieved. One important problem that cannot be seen clearly in figure 10.15 is that the resulting distributions still have very long tails. These tails represent probes that either occur very rarely or very frequently, and thus hinder the performance of the algorithm. To overcome this problem a procedure of post­screening is used. It uses the hybridization data to screen out certain probes that deviate significantly from the same ­ rate model. Only those probes which well fit the same ­ rate model are subsequently used by the mapping algorithm. As hybridization data is obtained after probe pre-selection, most probes already conform with the model, and so there is little loss of usable hybridization information. The post­screening process uses the number of actual probe occurrences in the hybridization data and the noise parameters. This technique works well when the noise estimate is good. If no good noise estimates are available, one would probably do better by computing a histogram of the number of hybridizations, and keeping only the probes in the central part of the histogram.

  

Figure: Influence of clone length variability. The x axis represents the maximal variability from the average clone sized length. Clone lengths were uniformly distributed in this range. The graphs show good performance with a variability of up to about 15000bp, or $37.5\%$.

  

Figure 10.14: Histogram of the number of 8 ­- mer probe occurrences along a genome section of length 1MB.

  

Figure 10.15: Histograms of the number of probe occurrences on a genome section of length 1MB, when using only probes with an average number of occurrences (between 0.9 and 1.1 of average) as estimated from a different genome section of length 1MB (730KB for human) of the same organism

 

Table: Results of the mapping algorithm with probe pre­selection on real sequence data. The three lines for each organism correspond to: (1) No post­screening, (2) Post­screening on the 500 original probes (leaving about 300 screened probes), and (3) 500 post­screened probes (requiring more to begin with). The screened probes were chosen out of a pre­selected sample of probes occurring within $10\%$ of the mean on a different genome section of the same organism. The post­screened probes are estimated to occur within $10\%$ of the mean frequency on the target genome section too. Averages and standard deviations are based on 1000 simulations in each scenario. PS: post­screening.

 

organism	test type	% maps with errors
Random	no post­screening
Random	PS ­ 500 probes before
Random	PS ­ 500 probes after	$0.0 \pm 0.0$
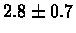Bacterium	no post­screening	$60.6 \pm 2.2$
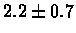Bacterium	PS ­ 500 probes before	$20.6 \pm 1.8$
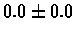Bacterium	PS ­ 500 probes after	$10.8 \pm 1.4$
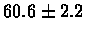Yeast	no post­screening	$20.4 \pm 1.8$
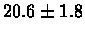Yeast	PS ­ 500 probes before	$4.0 \pm 0.9$
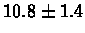Yeast	PS ­ 500 probes after	$1.2 \pm 0.5$
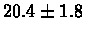C. Elegans	no post­screening	$34.6 \pm 2.1$
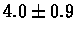C. Elegans	PS ­ 500 probes before	$7.4 \pm 1.2$
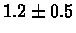C. Elegans	PS ­ 500 probes after	$0.0 \pm 0.0$
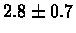Human	no post­screening	$88.2 \pm 1.4$
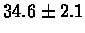Human	PS ­ 500 probes before	$12.6 \pm 1.5$
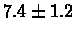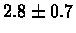Human	PS ­ 500 probes after	$0.0 \pm 0.0$