 where
N(t) = number of events until time t
where
N(t) = number of events until time t
| (10.2) |
 where
N(t) = number of events until time t
where
N(t) = number of events until time t
| (10.2) |
| (10.3) |
 are distributed uniformly and
independently in [0,t].
Assume clone length L, genome length G, and choose N clones
at random. What is the expected fraction of the genome covered by
clones?
For a random point b, and an arbitrary clone C the probability
of the point b being included in the clone c is given by:
are distributed uniformly and
independently in [0,t].
Assume clone length L, genome length G, and choose N clones
at random. What is the expected fraction of the genome covered by
clones?
For a random point b, and an arbitrary clone C the probability
of the point b being included in the clone c is given by:
| (10.4) |
| (10.5) |
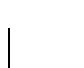 and
and  .
.
| (10.6) |
|
| (10.8) |
| (10.9) |
| (10.10) |
| (10.11) |
| (10.12) |
| (10.13) |