


Next: The Breakpoint Graph
Up: An Algorithm for Sorting
Previous: Group Theory Viewpoint
Definitions
Let
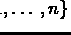 denote a permutation of
denote a permutation of
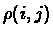 .
Augment
.
Augment  to a permutation on n+2 vertices
by adding
to a permutation on n+2 vertices
by adding 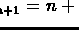 and
and
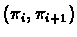 to it. A pair
to it. A pair
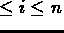 ,
,
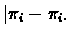 is called a gap. Gaps are
classified into two types: A gap
is called a gap. Gaps are
classified into two types: A gap
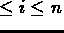 is called a
breakpoint of
is called a
breakpoint of  if
if
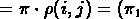 ;
otherwise, it is called an adjacency of
;
otherwise, it is called an adjacency of  .
We denote by
.
We denote by 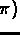 the number of breakpoints in
the number of breakpoints in  .
Recall from section 11.4.1 that a reversal,
.
Recall from section 11.4.1 that a reversal,
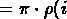 ,
on a permutation
,
on a permutation  transforms
transforms  to
to
We say that a reversal 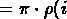 acts on the gaps
acts on the gaps
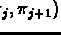 and
and
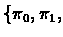 .
.
Itshack Pe`er
1999-03-16