


Next: Hurdles
Up: An Algorithm for Sorting
Previous: The Breakpoint Graph
The Overlap Graph
Two intervals on the real line overlap if their intersection
is nonempty but neither one of them properly contains the other.
An interval overlap graph is a graph G(V,E), for which
there is an assignment of an interval to each vertex such that two
vertices are adjacent if and only if the corresponding intervals
overlap. For a permutation  ,
we associate with a gray edge
,
we associate with a gray edge
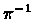 the interval [i,j]. The overlap graph of a
permutation
the interval [i,j]. The overlap graph of a
permutation  ,
denoted
,
denoted 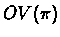 ,
is the interval overlap
graph of the gray edges of
,
is the interval overlap
graph of the gray edges of 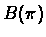 .
Namely, the vertex set of
.
Namely, the vertex set of
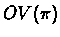 is the set of gray edges in
is the set of gray edges in 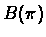 ,
and two vertices
are connected if the intervals associated with their gray edges
overlap. We shall identify a vertex in
,
and two vertices
are connected if the intervals associated with their gray edges
overlap. We shall identify a vertex in 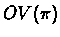 with the edge it
represents and with its interval in the representation. Thus, the
endpoints of a gray edge are actually the endpoints of the
interval representing the corresponding vertex in
with the edge it
represents and with its interval in the representation. Thus, the
endpoints of a gray edge are actually the endpoints of the
interval representing the corresponding vertex in 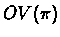 .
A
connected component of
.
A
connected component of 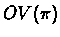 that contains an oriented edge is
called an oriented component, otherwise, it is called an
unoriented component. Figure 11.9(c) shows
the interval overlap graph for
that contains an oriented edge is
called an oriented component, otherwise, it is called an
unoriented component. Figure 11.9(c) shows
the interval overlap graph for
 .
It has
only one oriented component. Figure 11.10(b) shows
the overlap graph of the permutation
.
It has
only one oriented component. Figure 11.10(b) shows
the overlap graph of the permutation
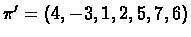 ,
which
has two connected components, one oriented and the
other unoriented.
,
which
has two connected components, one oriented and the
other unoriented.
Figure:
a) The
breakpoint graph of
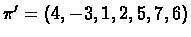 .
.
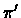 was obtained
from
was obtained
from  of figure 11.9 by the reversal
of figure 11.9 by the reversal
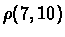 ;
or, equivalently, by the reversal defined by the
gray edge (2,3). b) The overlap graph of
;
or, equivalently, by the reversal defined by the
gray edge (2,3). b) The overlap graph of 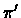 .
.
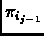 |
Lemma 11.9
The reversal acting on a gray edge flips the orientation of all
edges overlapping it, leaving all other edges unchanged.
We shall see that any connected component which is oriented can be
transformed by a series of reversals to a set of trivial connected
components that correspond to the identity permutation. The unoriented
connected components impose a problem for us since we cannot split
any of their cycles, nor delete any of their breakpoints by applying a
single reversal.
In some cases we can eliminate unoriented components. This is done
either by applying a reversal that does not increase the number of
cycles, but rather transforms some of the edges to
oriented edges, or by applying a reversal that merges two or more
unoriented connected components into one oriented component.
The above idea for eliminating unoriented components allows a
characterization of the unoriented components, on which we have
to spend an extra reversal operation. We denote these components
as hurdles. A more accurate description follows.



Next: Hurdles
Up: An Algorithm for Sorting
Previous: The Breakpoint Graph
Itshack Pe`er
1999-03-16