


Next: Finding a Happy Clique
Up: An Algorithm for Sorting
Previous: Happy Cliques
Implicit Representation of the Overlap Graph
Note that an explicit representation of the overlap graph uses
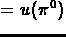 space, and since the neighborhood of a vertex may be
of size
space, and since the neighborhood of a vertex may be
of size 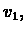 vertices (and
vertices (and
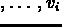 edges), it seems
we need to perform
edges), it seems
we need to perform
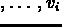 steps
per reversal, finally reaching a time bound of
steps
per reversal, finally reaching a time bound of
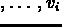 .
We shall therefore use an implicit representation of the
overlap graph, constructed as follows:
We assume that the input is given as a sequence of n signed
integers representing
.
We shall therefore use an implicit representation of the
overlap graph, constructed as follows:
We assume that the input is given as a sequence of n signed
integers representing  .
Initially the permutation
.
Initially the permutation
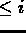 is constructed as described in
Section 11.4.4 and stored in an array. The
array holds n intervals and 2n endpoints, thus it is linear in
size. We also construct an array representing
is constructed as described in
Section 11.4.4 and stored in an array. The
array holds n intervals and 2n endpoints, thus it is linear in
size. We also construct an array representing 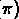 .
It is
straightforward to verify that with these two arrays we can
determine, in constant time, for each element in
.
It is
straightforward to verify that with these two arrays we can
determine, in constant time, for each element in  whether it
is a left or a right endpoint of a gray edge. In case the
element is an endpoint of a gray edge we can also find the other
endpoint and check whether the edge is oriented in constant time.
Finding whether two edges overlap is also trivial in constant time.
Thus the arrays
whether it
is a left or a right endpoint of a gray edge. In case the
element is an endpoint of a gray edge we can also find the other
endpoint and check whether the edge is oriented in constant time.
Finding whether two edges overlap is also trivial in constant time.
Thus the arrays  and
and 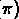 comprise a representation of
comprise a representation of
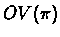 .
Our algorithm will maintain these two arrays while carrying out
the reversals that it finds. The time to update the arrays
is proportional to the length of the interval
being reversed, which is O(n).
It is easy to produce a list of
the intervals in the representation of
.
Our algorithm will maintain these two arrays while carrying out
the reversals that it finds. The time to update the arrays
is proportional to the length of the interval
being reversed, which is O(n).
It is easy to produce a list of
the intervals in the representation of 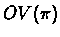 sorted
by either left or right endpoint from the arrays
sorted
by either left or right endpoint from the arrays
 and
and 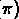 .
It is also possible to maintain them without increasing the
asymptotic time bound of the algorithm.
In practice it may be faster to maintain such
lists instead of, or in addition to
.
It is also possible to maintain them without increasing the
asymptotic time bound of the algorithm.
In practice it may be faster to maintain such
lists instead of, or in addition to  and
and 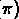 .
.



Next: Finding a Happy Clique
Up: An Algorithm for Sorting
Previous: Happy Cliques
Itshack Pe`er
1999-03-16