The polynomial solution

Luckily, a polynomial solution for this problem exists, due to Pevzner [13]. Define another directed graph G=(V,E). This time the vertices will be (k-1)-mers. An edge e=(v₁,v₂) will exist if the two (k-1)-mers form a k-mer that was reported present in the sequence. This graph is called the de-Bruijn graph of the sequence.

  

Figure 12.2: The (k-1)-mer graph constructed given the k-spectrum (k=3) in equation 12.1

For instance, if

$$S = \{ AAA,AAC,ACA,CAC,CAA,ACG,CGC,GCA,ACT,CTT,TTA,TAA \}$$ (12.1)

then the corresponding graph will be the one in figure 12.2. The mathematical problem here is to find an Euler path, that is a path that uses each edge once, and only once. For example, the sequence

T=ACAAACGCACTTAA

is a solution to the instance whose graph is depicted in figure 12.2, corresponding to the Euler path

$$AC \rightarrow CA \rightarrow AA \rightarrow AA \rightarrow A... ... \rightarrow CT \rightarrow TT \rightarrow TA \rightarrow AA$$

in that graph. It should be noted that for this construction, it is very important to know whether a given k-mer occurs more than once in the target sequence. For instance, if ACA occurs two times in S, then there should be two edges between AC and CA. Otherwise, our solution will not be correct. While this solution is mathematically elegant, there are several problems with using it in true biological context:

1.

For some graph configurations, there is more than once Euler path. In such cases we will not be able to reconstruct the sequence. For an example of such a graph, see figure 12.3.

2.

As in all biological experiments, the spectrum we measure contains a large proportion of errors. This solution is not robust enough to handle them.

3.

A related problem is that of edge multiplicity. We can consider ourselves lucky to know with certainty whether a certain k-mer occurs in our sequence. In most cases we have no way of knowing exactly how many times it occurs.

  

Figure 12.3: A graph with multiple Euler paths: an Euler path may traverse the top triangle either before or after the bottom one.

The only problem which we shall address here is the first one - the problem of the graph representing more than one possible sequence. This ambiguity corresponds to a branching in the graph.

Problem 12.2   Expected length of unique reconstruction
QUESTION: For a given branching probability p, on the ``all-k-mers'' chip C(k), what is the expected length of an unambiguously reconstructed sequence?

The solution to this problem is due to Lipschutz and Pevzner [14]. The analysis will not be given here.

Theorem 12.3   [14]
Expected length of unambiguous reconstruction $\approx \frac{1}{3}4^{k}p$

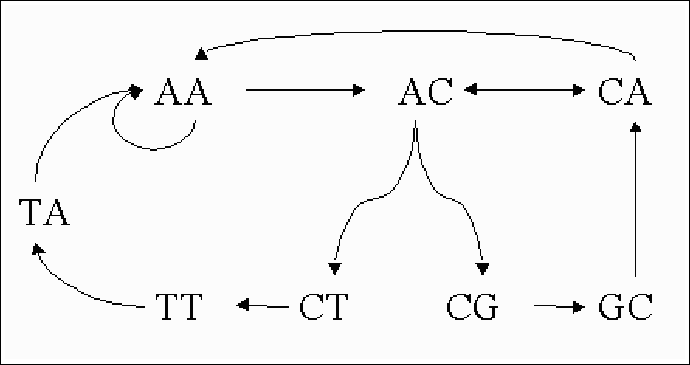
If we take k=8, which is a practical length, and p=0.01, we get that the expected length of the reconstructed sequence is 210 bases. When one considers genes, that can be several thousands of bases long, this is obviously not good enough. Some other chip designs achieve a somewhat better result, but these designs are only theoretical. They are usually very difficult or impossible to manufacture, and cannot be used in true biological context. Sadly, then, sequencing based on hybridization is not a real alternative to standard sequencing.