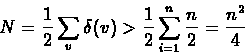Next: Refinements
Up: The HCC Algorithm
Previous: Clustering
Properties of HCC clustering
Theorem 12.5
The diameter of each cluster is smaller than or equal to 2. That is, the
distance between two vertices is at most 2.
Proof:Let k(G) be the size of the minimum cut, let d(v) denote the degree of v
and
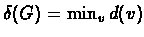 .
Observe that
.
Observe that
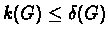 :
suppose to
the contracy that d(v)<k(G) for some v, then the cut
:
suppose to
the contracy that d(v)<k(G) for some v, then the cut
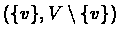 contradicts minimality of k(G). Furthermore, if G is a cluster
reported by the HCC algorithm, then according to the ``if'' statement in the
algorithm
contradicts minimality of k(G). Furthermore, if G is a cluster
reported by the HCC algorithm, then according to the ``if'' statement in the
algorithm
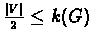 (otherwise G would have been divided in
two by HCC). Therefore,
(otherwise G would have been divided in
two by HCC). Therefore,
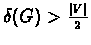 .
Consider two vertices v1 and v2 in G. If they are neighbors, then
surely the theorem holds for them. Let us therefore assume that they are not
neighbors. From the previous inequality, each one of these vertices has more
than
.
Consider two vertices v1 and v2 in G. If they are neighbors, then
surely the theorem holds for them. Let us therefore assume that they are not
neighbors. From the previous inequality, each one of these vertices has more
than
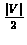 neighbors in G. Therefore, they must have a common
neighbor, since the total number of vertices in the graph is |V|, and
therefore the total number of their neighbors cannot exceed |V|-2.
While we have proven that each highly connected cluster has a small diameter,
the converse does not necessarily hold. That is, G may have a subgraph, with
diameter 2 that is not a highly connected component.
neighbors in G. Therefore, they must have a common
neighbor, since the total number of vertices in the graph is |V|, and
therefore the total number of their neighbors cannot exceed |V|-2.
While we have proven that each highly connected cluster has a small diameter,
the converse does not necessarily hold. That is, G may have a subgraph, with
diameter 2 that is not a highly connected component.
Lemma 12.6
Let
S be a set of edges forming a minimum cut in the graph
G=(
V,
E). Let
H and
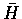
be the induced subgraphs obtained by removing
S from
G,
where
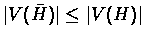
.
If
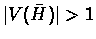
then
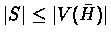
,
with equality only if
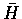
is a clique.
The lemma implies that if a minimum cut S in G=(V,E) satisfies
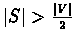 then S splits the graph into a single vertex
then S splits the graph into a single vertex 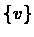 and
and
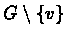 .
This shows us that using a stronger stopping criterion
for the algorithm, i.e.,
.
This shows us that using a stronger stopping criterion
for the algorithm, i.e.,
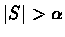 ,
for
,
for
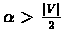 will be
detrimental for clustering: Any cut of value
will be
detrimental for clustering: Any cut of value
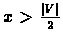 separates
only a singleton from the current graph.
separates
only a singleton from the current graph.
Theorem 12.7
Let
S be a minimum cut in the graph
G=(
V,
E) where
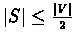
.
Let
H and
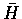
be the connected induced subgraphs
obtained by removing
S from
G, where
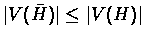
.
If
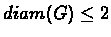
then (1) every vertex in
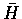
is incident on
S,
(2)
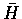
is a clique.
It can be shown, using this theorem, that the union of two vertex sets split
by any step of HCC is unlikely to induce a graph with diameter 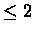 if
noise is random, and the vertex sets are not too small. Another property of the
solution is given by:
if
noise is random, and the vertex sets are not too small. Another property of the
solution is given by:
Theorem 12.8
1. The number of edges in a highly connected subgraph is quadratic.
2. The number of edges removed by each iteration of the HCC algorithm is at
most linear.
Proof:Let n be the number of edges in the graph. Then:
1. As we have seen before,
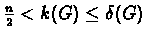 .
Since the
rank of each vertex is
.
Since the
rank of each vertex is
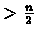 ,
the total number of edges is
,
the total number of edges is
2. The algorithm removes the edges forming the minimal cut S, only if
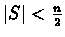 .
Therefore, obviously the number of removed edges is linear.
.
Therefore, obviously the number of removed edges is linear.



Next: Refinements
Up: The HCC Algorithm
Previous: Clustering
Itshack Pe`er
1999-03-16