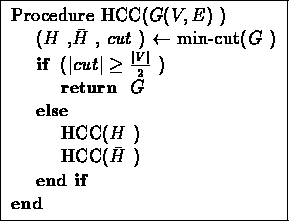Clustering

Now that we have the fingerprints of the different cDNA, it remains to be seen how we can sort them into groups that (hopefully) represent the same gene. For the specific problem of clustering cDNA fingerprints, several approaches were suggested previously. Drmanac et al. [15] construct clusters according to connected components in the similarity graph. However, even with a low false positives rate in the data, such an algorithm would incorrectly merge true clusters. Meyer-Ewert, Mott and Lehrach [10] construct clusters according to maximal cliques. This approach does not work well either, since computing all maximal cliques is computationally difficult. Moreover, a high false negative rate may break large clusters into many maximal cliques, with a hard-to-detect overlap structure. Milosavljevic et al. [12] construct clusters using a greedy algorithm. Like most greedy approaches, this algorithm cannot well handle high noise levels, and the quality of its results is very sensitive to the starting point. The algorithm we will describe here is due to Shamir et al. [6]. Once again we will use graphs as our main tool. Let us define a graph G=(V,E), where the vertices are the extracted cDNA, and an edge e=(v₁, v₂) exists if v₁ and v₂ have similar fingerprints (for discussing the definition of similar fingerprints, the interested reader is referred to [6]). Recall the following definitions:

1.

The   connectivity k(G) of a graph G is the minimum number of edges whose removal results in a disconnected graph. If k(G)=l then G is said to be   l-(edge)-connected.

2.

A   cut in G is a set of edges who removal disconnects the graph. A   minimum cut is a cut with minimum number of edges. If C is a minimum cut set of a non-trivial graph G, then |C|=k(G). Hence, a k-connected graph is a nontrivial graph in which the size of a minimum cut is k.

Had the similarity graph perfectly represented the cluster structure, each cluster would have formed a clique, as all members of a cluster are highly similar, and no two clusters would have been connected by an edge. In practice, searching for cliques in the graph would fail on two accounts: First, finding maximum cliques is computationally intractable [5]. Second, and more important, real data matrices (and cDNA hybridization matrices in particular) contain many errors. In terms of the similarity graph, false negatives correspond to missing edges between vertices in the same cluster, and false positive errors correspond to extra edges between vertices of different clusters. In cDNA fingerprinting, errors in the hybridization data generate inexact fingerprinting, leading in turn to errors in the similarity graph. That error rate is very high: The false negative rate in the similarity graph is above 50% and the false positive rate is smaller but still significant. A key definition for our approach is the following: A graph G with n>1 vertices is called highly connected if 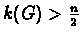$k(G)>\frac{n}{2}$. 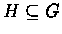A   highly connected component (HCC) is an induced subgraph $H \subseteq G$ such that H is highly connected. The algorithm identifies highly connected components of a given parameter graph. 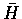The algorithm given here assumes that the procedure min-cut(G) returns H, $\bar{H}$ and C, where C is a minimum cut set which separates G into the subgraphs H and $\bar{H}$.

  

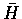Figure 12.4: The basic HCC algorithm

The algorithm is given in figure 12.4. It works as follows: In each iteration, it finds the minimum cut in the graph, and separates the graph into two subgraphs. If the current graph is highly connected, the algorithm stops (as it has found a cluster). Otherwise, it recursively continues processing each of the two subgraphs.