


Next: End free-space alignment
Up: Local Alignment
Previous: Motivation
Computing local alignment
Given a pair of indices
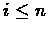 and
and
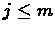 , the local suffix alignment problem is
finding a (possibly empty) suffix
, the local suffix alignment problem is
finding a (possibly empty) suffix 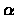 of
of
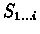 and a
(possibly empty) suffix
and a
(possibly empty) suffix 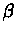 of
of
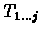 such that the
value of their alignment is the maximum over all values of
alignments of suffixes of
such that the
value of their alignment is the maximum over all values of
alignments of suffixes of
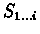 and
and
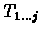 .
We use V(i,
j) to denote the value of the optimal local suffix alignment for
a given pair i, j of indices.
.
We use V(i,
j) to denote the value of the optimal local suffix alignment for
a given pair i, j of indices.
We choose the weights of the editing operations as:
The algorithm needs to:
- 1.
- Find maximum similarity between suffixes of
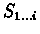 and
and
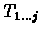 .
.
- 2.
- Discard the prefixes
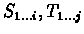 whose similarity is
whose similarity is 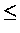 0, and therfore decreases the overall similarity.
0, and therfore decreases the overall similarity.
- 3.
- Find the best indices i*, j* of S and T respectively after which the similarity only decreases.
Note that any extension of the optimal solution either to the right of to the left decreases the overall similarity.
Recursive definition:
The base condition will be:
V(i, 0) = 0 and
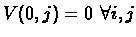 since we can always choose an empty suffix.
since we can always choose an empty suffix.
For i > 0 and j > 0 the proper recurrence for V(i, j)is
Compute i*, j* so that:
Observe that the recurrence for computing local suffix alignment is almost identical to the one used for computing global alignment. The only difference
is the inclusion of zero in the case of local suffix alignment. In both global alignment and local suffix alignment of prefixes
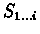 and
and
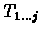 ,
the terminating characters of any alignment are specified, but in the case of local suffix alignment, any number of initial characters can be ignored.
,
the terminating characters of any alignment are specified, but in the case of local suffix alignment, any number of initial characters can be ignored.
The zero in the recurrence implements this, 'restarting' the recurrence. Adding 0 to the maximization makes sure that negative prefixes are discarded from the computation.
Adding the '0' to the constraint only handles mismatched prefixes, there's still a need to determine, when should a computation of a transformation be stopped, so that the similarity value will not decrease.
Therefore, after computing the table of V(i, j) values, and there's a need to search for
a cell with the maximal value and ignore all table entries from that point on.
Example 2.14
Figure
2.3 illustrates the calculation of the

entries table for the two strings taken
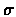
as 2 for match and -1 for mismatch.
Figure 2.3:
finding local alignment
|
|
As usual, pointers are created while filling in the values of the table. After cell
(i*, j*) is found, the substrings 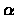 and
and 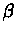 giving the optimal local
alignment of S and T are found by tracing back the pointers from cell
(i*, j*) until reaching an entry
(i', j') that has value zero. Then the optimal local alignment substrings are
giving the optimal local
alignment of S and T are found by tracing back the pointers from cell
(i*, j*) until reaching an entry
(i', j') that has value zero. Then the optimal local alignment substrings are
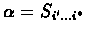 and
and
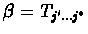 .
As it seems from here, space complexity will be O(mn), we will show that only O(m) space is needed:
.
As it seems from here, space complexity will be O(mn), we will show that only O(m) space is needed:
Lemma 2.15
The optimal local alignment of two strings
S and
T can be computed in linear space.
Proof:The optimal local alignment of S and T identifies substrings 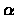 and
and 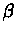 whose global alignment has maximum value over all pairs of substrings. Hence, if
whose global alignment has maximum value over all pairs of substrings. Hence, if 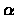 and
and
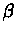 can be found using only linear space, then their actual alignment can be found in
linear space, using Hirschberg's method for global alignment. The value of the optimal local alignment is found in cell
i*, j*. Those indices specify the terminating points
of the strings
can be found using only linear space, then their actual alignment can be found in
linear space, using Hirschberg's method for global alignment. The value of the optimal local alignment is found in cell
i*, j*. Those indices specify the terminating points
of the strings 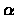 and
and 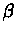 .
The values of each row can be computed in a row wise
fasion and the algorithm must store values for only two rows at a time. Hence, the end positions
(i*, j*) can be computed in linear space. To find the starting position of the two
substrings, the algorithm can execute the reverse dynamic programing using linear space (the details are left as an exercise).
.
The values of each row can be computed in a row wise
fasion and the algorithm must store values for only two rows at a time. Hence, the end positions
(i*, j*) can be computed in linear space. To find the starting position of the two
substrings, the algorithm can execute the reverse dynamic programing using linear space (the details are left as an exercise).
Complexity :
- Time Complexity - since it takes constant number of operation per cell to compute
V(i, j), it takes only O(mn) time to fill in the entire
table. The search for V(i*, j*) requires only O(nm) time as well. Hence the total time complexity is O(nm).
- Space Complexity - As shown in lemma local alignment, the space complexity is O(m).



Next: End free-space alignment
Up: Local Alignment
Previous: Motivation
Itshack Pe`er
1999-01-03
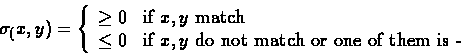
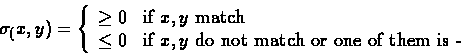
![]() since we can always choose an empty suffix.
since we can always choose an empty suffix.
![]() and
and
![]() ,
the terminating characters of any alignment are specified, but in the case of local suffix alignment, any number of initial characters can be ignored.
,
the terminating characters of any alignment are specified, but in the case of local suffix alignment, any number of initial characters can be ignored.
![]() and
and ![]() giving the optimal local
alignment of S and T are found by tracing back the pointers from cell
(i*, j*) until reaching an entry
(i', j') that has value zero. Then the optimal local alignment substrings are
giving the optimal local
alignment of S and T are found by tracing back the pointers from cell
(i*, j*) until reaching an entry
(i', j') that has value zero. Then the optimal local alignment substrings are
![]() and
and
![]() .
As it seems from here, space complexity will be O(mn), we will show that only O(m) space is needed:
.
As it seems from here, space complexity will be O(mn), we will show that only O(m) space is needed: