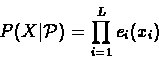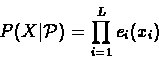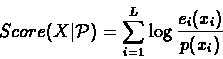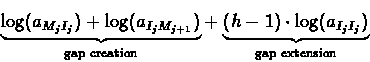Next: Aligning Sequences to a
Up: Profile Alignment
Previous: Profile Alignment
Profile HMMs
HMMs can be used for aligning a string versus a given profile,
thus helping us to solve the multiple alignment problem.
We define a profile
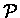 of length L, as a set of
probabilities, consisting of, for each
of length L, as a set of
probabilities, consisting of, for each
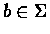 and
and
 ,
the probability ei(b) of observing the symbol b
at the
,
the probability ei(b) of observing the symbol b
at the
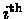 position. In such a case the probability of
a string
position. In such a case the probability of
a string
 given the profile
given the profile
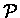 will be:
will be:
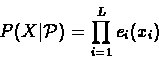 |
(6.39) |
We can calculate a likelihood score for the ungapped alignment of
X against the profile
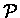 :
:
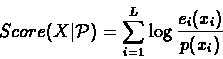 |
(6.40) |
where p(b) is the background frequency of occurrences of the
symbol b.
This leads to a definition of the following HMM, with the
match states
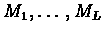 which correspond to matches
with the profile. All those states are sequentially linked (i.e.,
each match state Mj is linked to its successor Mj+1) as
shown in figure 6.2. The emission
probability of the symbol b from the state Mj is of course
ej(b).
which correspond to matches
with the profile. All those states are sequentially linked (i.e.,
each match state Mj is linked to its successor Mj+1) as
shown in figure 6.2. The emission
probability of the symbol b from the state Mj is of course
ej(b).
Figure 6.2:
Match states
in a profile HMM
|
|
To allow insertions, we will add the insertion states
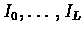 to the model. We shall assume that:
to the model. We shall assume that:
Each insertion state Ij has an link entering from the
corresponding match state Mj, a leaving link towards the next
match state Mj+1 and also has a self-loop (see figure
6.3). Assigning the appropriate
probabilities for those transitions corresponds to the application
of affine gap penalties, since the overall contribution of a gap
of length h to the logarithmic likelihood score is:
Figure 6.3:
Profile
HMM with an insertion state
|
|
To allow deletions as well, we add the deletion states
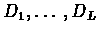 .
These states cannot emit any symbol and are
therefore called silent (Note that the begin/end states
are silent as well). The deletion states are sequentially linked,
in a similar manner to the match states and they are also
interleaved with the match states (see figure
6.4).
.
These states cannot emit any symbol and are
therefore called silent (Note that the begin/end states
are silent as well). The deletion states are sequentially linked,
in a similar manner to the match states and they are also
interleaved with the match states (see figure
6.4).
Figure 6.4:
Profile
HMM with deletion states
|
|
To model both insertions and deletions, we have to add a link from
Dj to Ij and a link from Ij to Dj+1.
The full HMM for modeling the profile
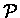 of length L
is comprised of L layers, each layer has three states Mj,
Ij and Dj. To complete the model, we add begin and
end states, connected to the layers as shown in figure
6.5. This model is due to Haussler
et al [5].
of length L
is comprised of L layers, each layer has three states Mj,
Ij and Dj. To complete the model, we add begin and
end states, connected to the layers as shown in figure
6.5. This model is due to Haussler
et al [5].
Figure 6.5:
Profile
HMM for global alignment
|
|



Next: Aligning Sequences to a
Up: Profile Alignment
Previous: Profile Alignment
Itshack Pe`er
1999-01-24